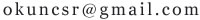a^2>b^2+c^2,a<b+c,a,b,c>0
判别=[2√(b^2+c^2)]^2-4*(a^2+bc)
=4(b^2+c^2)-4a^2-4bc
=4(b^2+c^2-a^2)-4bc
<0
无实数根
已知三角形ABC的三边分别为abc,且关于X的方程
(b-X)²-4(a-X)(c-X)=0===>b²-2bX+X²-4(X²-aX-cX+ac)=0 ===>-3X²+(4a+4c-2b)X+b²-4ac=0 ∴Δ=(4a+4c-2b)²-4*(4ac-b²)*3 =16a²+16c²+4b²+32ac-16bc-16ab-48ac+12b²=16a²+...
...且方程(a⊃2;+b⊃2;+c⊃2;)x⊃2;+2(a+b+
因为方程(a²+b²+c²)x²+2(a+b+c)x+3=0有两个相等的实数根,所以判别式=0,即 [2(a+b+c)]^2-4(a^2+b^2+c^2)*3=0,(a+b+c)^2-3(a^2+b^2+c^2)=0,a^2+b^2+c^2+2ab+2bc+2ac-3a^2-3b^2-3c^2=0,2a^2+2b^2+2c^2-2ab-2bc-...
...方程b⊃2;x⊃2;+(b⊃2;+c⊃2;-a⊃2;)x+c⊃
证无实根就是证△小于零 △=(b²+c²-a²)²-4c²b²=平方差公式最终化为=(b-c-a)(b-c+a)(b+c+a)(b+c-a)因为他们是三角形三边,两边和大于第三遍,两边差小于第三边,不就知道是小于零了嘛 ...
...试判断关于x的一元二次方程a平方x平方+(a平方+b平方-c平方)x+b...
解:由题意得:因为 a,b,c为三角形的三边 所以 a+b>c 所以 a平方+b平方>c平方 且 a平方+b平方-c平方>0并a>0,b>0,c>0 重组等式 a²x²+(a²+b²-c²)x+b²=0 得 x(a²x+a²+b²-c²)+b²=0 已知...
...2;+b⊃2;+c⊃2;=ab+bc+ac,试判断三角形ABC的形状(过程
这是一个等边三角形。对于类似的题目,我们把它们叫做“轮换式”,也就是abc三个字母是可以轮换而不改变等式的性质的。这种情况下,可以推测a=b=c 严格的证明过程如下:这是一个等边三角形。
...形的三条边,求证:关于x的方程b平方x平方+(b平方+c平方—a平方)x+c...
证明:∵方程b²x²+(b²+c²-a²)x+c²=0的判别式 △=(b²+c²-a²)²-4b²c²=(b²+c²-a²+2bc)(b²+c²-a²-2bc)=((b+c)²-a²)((b-c)²-a²)=(b+c...
已知关于x的一元二次方程(b-c)x⊃2;;+(c-b)x+(a+b)=0有两个相等的实...
原式应为:(b-c)x²+(c-a)x+(a-b)=0 ,∵ 方程有两个相等的实数根,∴ b-c≠0 ,判别式 △=0 ,∴ (c-a)²-4(b-c)(a-b) = 0 c²-2ac+a²-4ab+4ac+4b²-4bc = 0 ,a²+2ac+c²-4ab+4b²-4bc = 0 ,4b²-...
若实数abc是三角形的三边,试判断方程b²x²+(b²+c²-a²...
在一元二次方程b²x²+(b²+c²-a²)x+c²=0中,Δ(根判别式)=b²-4ac =(b²+c²-a²)²-4b²c²=(b²+c²-a²)²-(2bc)²=(b²+c²-a²+2bc)(b²+c²-...
函数问题
即f(x)-(x+c)²≤0恒成立 即f(x)≤(x+c)²在x≥0时恒成立 得证 (2)f(c)-f(b)=c²+bc+c-b²-b²-c=(c²-b²)+(bc-b²)=(c+b)(c-b)+b(c-b)=(c+2b)(c-b)f(c)-f(b)-M(c²-b²)=(c-b)(c+2b-Mc-Mb...
数学题求解
0<2\/(2^x+1)<2 -2 < -2\/(2^x+1)< 0 所以-1<f(x)=1 - 2\/(2^x+1)<1 即f(x)的值域为(-1,1)(3)g(x)=x²\/2f(x)因为f(x)=(2^x-1)\/(2^x+1)f(-x)=[2^(-x)-1]\/[2^(-x)+1](分子分母同乘2^x)=[1-2^(-x)]\/[1+2^(-x)]= -f(x)所...