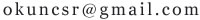∴ 1/3+2/3=1=0.3 …+0.6… =0.9…
∴1=0.9…
②∵0.3 …=3.3…/10=0.3 …/1=3.3…-0.3 …/10-1= 1/3
∴0.9…=9.9…/10=9.9…/1=9.9…-0.9…/10-1=9/9=1
参考资料:百度数学吧
本回答被提问者采纳0.99999999…为什么等于一
因为0.99999999…=9\/10+9\/100+9\/1000+.=1,这是无穷等比数列的和.
0.99999999…为什么等于一
因为0.99999999…=9\/10+9\/100+9\/1000+...=1,这是无穷等比数列的和。
为什么0.99999999…的无限循环与1相等?
第一种,最简单的:设x=0.9999999999999……,那么10x=9.99999999999……,得到 10x-x=9 得x=1 第二种,也很简单的:设x=0.999999999999……,那么x\/3=0.333333333333……=1\/3,得 x\/3=1\/3 x=1 第三种,稍微要绕一点脑筋:你用竖式计算1除以1(竖式应该会吧,小学学过的),不同的...
0.99999999的无限循环和1哪个大
很郑重地告诉你0.9……=1,这是由10进制本生的缺陷造成的。除了那方法还有其他方法的,比如极限,级数。你可以参考《陶哲轩实分析》这本书。在书的后面有非常具体的证明。
如何证明:0.9999…=1
无限循环小数化分数无限循环小数,先找其循环节(即循环的那几位数字),然后将其展开为一等比数列、求出前n项和、取极限、化简。例如:0.99999999……循环节为9 则0.9=9*10^(-1)+9*10^(-2)+……+9^10(-n)+……前n项和为:9*0.1(1-(0.1)^(n))\/(1-0.1)当n趋向无穷时(0...
为什么说0.9999999……… 等于1呢?
因此0.999999999...所指的是9的个数为无穷多个,这一点首先要明确。然后就可以用等比数列知识来证明上述结论。证明过程如下:0.999999999...=0.9+0.09+0.009+0.0009+...=0.9*(1-0.1^n)\/(1-0.1)=0.9\/(1-0.1)=1(其中n为无穷大)因此0.99999999...=1是成立的。
0.999999999……为什么等于1
因此在它后面一般都要指明9的个数是多少个。 因此0.999999999...所指的是9的个数为无穷多个,这一点首先要明确。然后就可以用等比数列知识来证明上述结论。证明过程如下: 0.999999999...=0.9+0.09+0.009+0.0009+...=0.9*(1-0.1^n)\/(1-0.1)=0.9\/(1-0.1)=1(...
为什么,零点九九九循环等于一
这应用到了数学的“极限”理论。首先,0.999999999……在数位的延长中无限接近一但还没到一,大家为了简化就将其=1。其次1\/9=0.11111……,根据推断,9\/9=0.111111111……x9=0.9999999……,可按理论来说,9\/9=1,故0.99999999……=1。应用到“极限”理论的还有计算圆的面积。
证明0.99999...=1
因此0.999999999...所指的是9的个数为无穷多个,这一点首先要明确。然后就可以用等比数列知识来证明上述结论。证明过程如下:0.999999999...=0.9+0.09+0.009+0.0009+...=0.9*(1-0.1^n)\/(1-0.1)=0.9\/(1-0.1)=1(其中n为无穷大)因此0.99999999...=1是成立的。参考资料:htt...
0.99999999……(无限循环)和1大大小
相等,证明:令0.9999999...(无限循环)=x (1)所以9.9999999...(无限循环)=10x (2)(2)-(1)得 9=9x x=1 所以0.9999999...(无限循环)=1